Презентация - Решение задач на применение аксиом стереометрии и их следствий

Слайд 1

Презентация урока по геометрии Тема: «Решение задач на применение аксиом стереометрии и их следствий»

Слайд 2

Данная презентация посвящена аксиомам стереометрии и следствиям из них. Может быть использована: в виде диагностики знаний обучающихся при завершении темы «Аксиомы стереометрии и следствия из них»; при организации работы по готовому чертежу, что способствует развитию быстрого интуитивного логического мышления; для развития устной и письменной математической речи.

Слайд 3

Решение задач на применение аксиом стереометрии и их следствий Выполнила: Соломина Наталья Васильевна преподаватель математики и информатики ГБПОУ «Вышневолоцкий медицинский колледж»

Слайд 4

Цель урока: Закрепить усвоение вопросов теории в процессе решения; Проверить уровень подготовленности обучающихся: - при решении задач на готовом чертеже; - путём проведения самостоятельной работы контролирующего характера

Слайд 5

Ход урока Ι. Организационный момент. ΙΙ. Устная работа.

Слайд 6

П о в т о р я е м
Каковы аксиомы стереометрии?

Слайд 7

А
В
С
ɑ
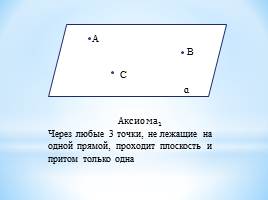
Аксиома 1 Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна

Слайд 8

Верно ли, что: Любые три точки лежат в одной плоскости; Да Любые четыре точки лежат в одной плоскости; Нет

Слайд 9

Любые четыре точки не лежат в одной плоскости; Нет Через любые три точки проходит плоскость, и притом только одна? Нет

Слайд 10

А
В
ɑ
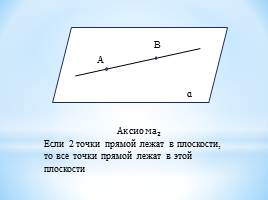
Аксиома 2 Если 2 точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

Слайд 11

Верно ли, что прямая лежит в плоскости данного треугольника, если она ( ответ обоснуйте): пересекает две стороны треугольника; проходит через одну из вершин треугольника?

Слайд 12

А
а
ɑ
ß
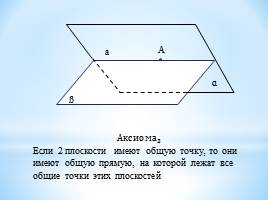
Аксиома 3 Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей

Слайд 13

В 1
С 1
А 1
Д 1
А
Д
В
С
К
М
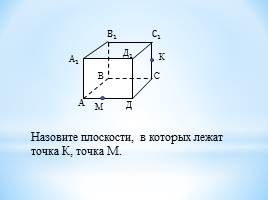
Назовите плоскости, в которых лежат точка К, точка М.

Слайд 14

Каковы следствия из аксиом?

Слайд 15

ɑ
а
М
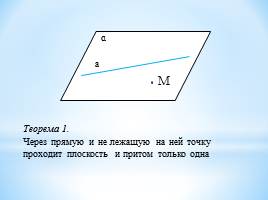
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна

Слайд 16

а
с
ɑ
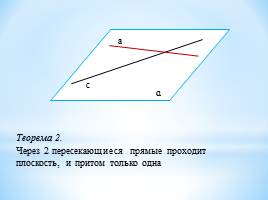
Теорема 2. Через 2 пересекающиеся прямые проходит плоскость, и притом только одна

Слайд 17

ΙΙΙ. Решение задач на готовом чертеже

Слайд 18

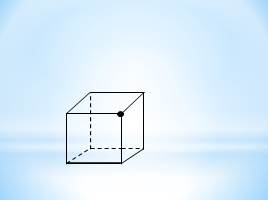
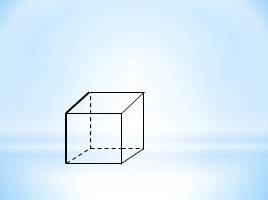
Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскостям грани куба.

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

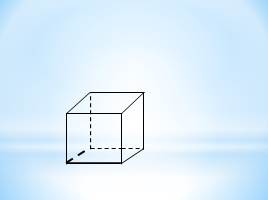
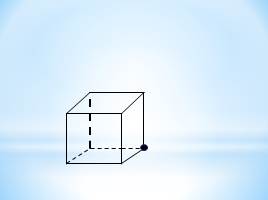
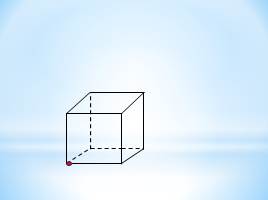
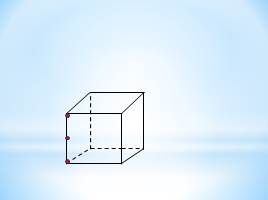
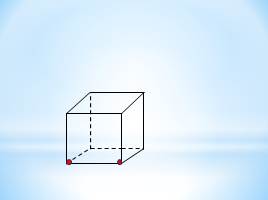
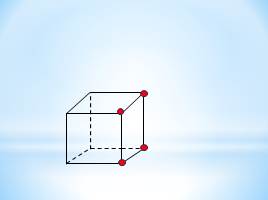
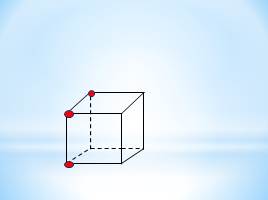
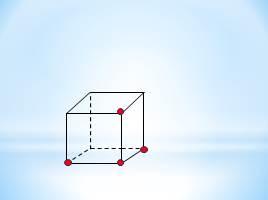
Сколько граней проходит через: а) одну, б) две, в) три, г) четыре точки, выделенные на рисунке куба? Сколько плоскостей можно провести через те же точки? Определится ли при этом положение плоскости однозначно? Ответ обоснуйте.

Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Ι/. Самостоятельная работа контролирующего характера Оценка «3» – пять любых заданий Оценка «4» – семь любых заданий Оценка «5» – девять любых заданий

Слайд 32

1.Какое из следующих утверждений верно? а) любые четыре точки лежат в одной плоскости; б) любые три точки не лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость; д) через любые три точки проходит плоскость, и притом только одна. Д

Слайд 33

2. Сколько общих точек могут иметь две различные плоскости? а) 2; б) 3; в) несколько; г) бесконечно много; д) бесконечно много или ни одной. Д

Слайд 34

3. Точки А, В, С лежат на одной прямой, точка Д не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось? а) 2; б) 3; в) 1; г) 4; д) бесконечно много. В

Слайд 35

4. Если три точки не лежат на одной прямой, то положение плоскости в пространстве они: а) не определяют в любом случае; б) определяют, но при дополнительных условиях; в) определяют в любом случае; г) ничего сказать нельзя; д) другой ответ. В

Слайд 36

5. Выберите верное утверждение: а) если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости; б) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна; в) через две пересекающиеся прямые плоскость провести нельзя; г) любые две плоскости не имеют общих точек; д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой. Б

Слайд 37

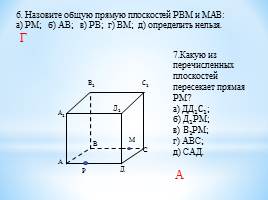
6. Назовите общую прямую плоскостей РВМ и МАВ: а) РМ; б) АВ; в) РВ; г) ВМ; д) определить нельзя. Г
В 1
С 1
В
А 1
Д 1
С
А
Д
Р
7.Какую из перечисленных плоскостей пересекает прямая РМ? а) Д Д 1 С 1 ; б) Д 1 РМ; в) В 1 РМ; г) АВС; д) САД. А
М

Слайд 38

8. Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном положении точки М и прямой с? а) никакого вывода нельзя сделать; б) на прямой с лежит точка М; в) через точку М прямая с не проходит; г) другой ответ. Г

Слайд 39

9. Прямые а и в пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и в. Что можно сказать о взаимном положении прямых а, в и с? а) все прямые лежат в разных плоскостях; б) прямые а и в лежат в одной плоскости, а прямая с в ней не лежит; в) все прямые лежат в одной плоскости; г) ничего сказать нельзя; д) прямая с совпадает с одной из прямых: или са, или св. В

Слайд 40

10. Точки А, В, С не лежат на одной прямой. МϵАВ, КϵАС, ХϵМК. Выберите верное утверждение: а) ХϵАВ, б) ХϵАС, в) ХϵАВС; г) точки Х и М совпадают; д) точки Х, К совпадают В

Слайд 41

/. Подведение итогов. 1.Собрать тетради с самостоятельной работой. 2.Оценки за урок. /Ι. Домашнее задание. Постройте изображение тетраэдра (треугольной призмы, четырёхугольной пирамиды, четырёхугольной призмы). Отметьте произвольно точки М, Н, К на рёбрах многогранника. Постройте сечение многогранника плоскостью (МНК).

Слайд 42

Спасибо за урок