Текст этой презентации
Слайд 1

ТЕМА УРОКА: «Четыре замечательные точки треугольника»
Слайд 2

Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.
Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороны.
Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему.
Слайд 3

Серединный перпендикуляр
Слайд 4
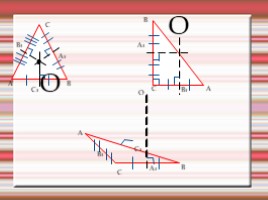
A
B
C
O
A
B
C
A
B
C
O
C1
A1
B1
B1
A1
A1
C1
B1
Слайд 5

ВЫВОД:
Серединные перпендикуляры в треугольнике пересекаются в одной точке
Слайд 6

Биссектрисы треугольника
Слайд 7
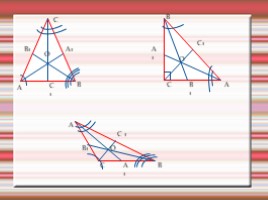
O
O
A
A
B
A
B
C
C
B
C
A1
B1
C1
A1
B1
C1
A1
B1
C 1
O
Слайд 8

ВЫВОД:
Биссектрисы треугольника пересекаются в одной точке
Слайд 9

Высоты треугольника
Слайд 10
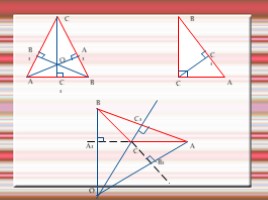
A
B
C
B1
A1
C1
A
C
B
C1
A
B
C
A1
B1
C1
O
O
Слайд 11

Вывод
Высоты треугольника пересекаются в одной точке.
Точку пересечения высот называют ортоцентром треугольника.
Слайд 12

Медианы треугольника
Слайд 13
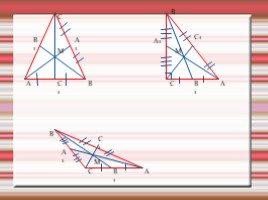
A
B
C
C1
A1
M
B1
A
C
B
A1
B1
C1
M
A
B
C
C1
B1
A1
M
Слайд 14

ВЫВОД:
Медианы треугольника пересекаются в одной точке и делятся ей в отношении 2:1 считая от вершины.
Точку пересечения медиан называют центром масс.
 Анаграммы
Анаграммы
 Неделя математики и физики
Неделя математики и физики
 Виртуальный музей истории математики
Виртуальный музей истории математики
 Красота математики, как и красота любой вещи
Красота математики, как и красота любой вещи
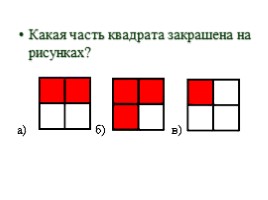 Обыкновенные дроби
Обыкновенные дроби















