Презентация - Логарифмы - История возникновения

Слайд 1

Логарифмы. История возникновения

Слайд 2

Что такое логарифм?
Логарифм положительного числа b по основанию а , где а > 0,а ≠ 1,называется показатель степени, в которую надо возвести число а, чтобы получить b/

Слайд 3

Слово ЛОГАРИФМ происходит от греческих слов  - число и  - отношение. переводится как отношение чисел, одно из которых является членом арифметической прогрессии, а другое геометрической.

Слайд 4

ЛОГАРИФМ число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление - вычитанием, возведение в степень - умножением и извлечение корней – делением.

Слайд 5

Впервые понятие логарифмов ввел английский математик Джон Непер. Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд "Описание удивительных таблиц логарифмов" опубликовал лишь в 1614 году.

Слайд 6

Джон Непер (1550-1617).

Слайд 7

Первые таблицы десятичных логарифмов были составлены в 1617 г. английским математиком Г.Бригсом. Многие из них были выведены с помощью выведенной Бригсом формулы. Изобретатели логарифмов не ограничились созданием логарифмических таблиц, уже через 9 лет после их разработки в 1623 г. Английским математиком Гантером была создана первая логарифмическая линейка. Она стала рабочим инструментом для многих поколений. В настоящее время мы можем находить значения логарифмов, используя компьютер. Так, в языке программирования BASIC с помощью встроенной функции можно находить натуральные логарифмы чисел.
Генри Бригс.
Бернард Гантер.

Слайд 8

Логарифмические линейки.

Слайд 9

Слайд 10

«Логарифмы бывают разные…»
Бригсов логарифм - то же, что десятичный логарифм. Назван по имени Г. Бригса.
Десятичный логарифм - логарифм по основанию 10. Десятичный логарифм числа а обозначают lgа.
Неперов логарифм - (по имени Дж. Непера), то же, что натуральный логарифм.
Натуральный логарифм-это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828

Слайд 11

Общее определение логарифмической функции и ее широкое обобщение дал Леонард Эйлер.
Логарифмическая функция.
Логарифмическая функция — это функция вида    где a>0, a≠1.

Слайд 12

Логарифмическая спираль.
Логарифмическая спираль представляет собой кривую, которую описывает точка, движущаяся вдоль луча, равномерно вращающегося вокруг своего начала таким образом, что логарифм расстояния от точки до начала луча возрастает прямо пропорционально углу поворота луча.
Эту кривую можно было бы назвать именем Декарта, поскольку впервые о ней говорится в одном из его писем. Однако подробное изучение её свойств было проведено только полвека спустя Якобом Бернулли. На его современников свойства произвели сильное впечатление. На каменной плите, водружённой на могиле этого знаменитого математика, изображены витки логарифмической спирали

Слайд 13

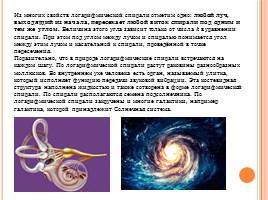
Из многих свойств логарифмической спирали отметим одно: любой луч, выходящий из начала, пересекает любой виток спирали под одним и тем же углом. Величина этого угла зависит только от числа k в уравнении спирали. При этом под углом между лучом и спиралью понимается угол между этим лучом и касательной к спирали, проведённой в точке пересечения. Поразительно, что в природе логарифмические спирали встречаются на каждом шагу. По логарифмической спирали растут раковины разнообразных моллюсков. Во внутреннем ухе человека есть орган, называемый улитка, который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и также сотворена в форме логарифмической спирали. По спирали располагаются семена подсолнечника. По логарифмической спирали закручены и многие галактики, например галактика, которой принадлежит Солнечная система.

Слайд 14

Применение логарифмов
Музыка Так называемые ступени темперированной хроматической гаммы (12- звуковой) частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях). Номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков

Слайд 15

Звезды, шум и логарифмы
Громкость шума и яркость звезд оцениваются одинаковым образом – по логарифмической шкале.

Слайд 16

Психология
Изучая логарифмы, ученые пришли к выводу о том, что величина ощущения пропорциональна логарифму величины раздражения.

Слайд 17

Зачем мы изучаем логарифмы?
Во-первых, логарифмы позволяют упрощать вычисления. Во-вторых, испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны.
Вывод: логарифмы – важные составляющие не только математики, но и всего окружающего мира, поэтому интерес к ним не ослабевает с годами и их необходимо продолжать изучать.