Презентация - Неевклидова геометрия

Слайд 1

МОУ «Бендерский теоретический лицей»
Выполнили : ученицы 8-Г класса Костинская Дарья и Коваджи Анастасия Учитель: Кожухарова Татьяна Александровна
Исследовательская работа на тему: «Неевклидова геометрия»

Слайд 2

Ученый должен идти по непроторенным путям, несмотря на препятствия. Н.И.Лобачевский

Слайд 3

Цель работы: Провести параллель между геометрией древнегреческого математика Евклида и русского математика Лобачевского Николая Ивановича.
Гипотеза: Существует ли неевклидова геометрия и ее отличия от школьной
Задача : изучить литературу и интернет-ресурсы по данной теме, рассмотреть различие между геометрией Евклида и геометрией Лобачевского

Слайд 4

Если две прямые образуют с третьей прямой внутренние односторонние углы, в сумме меньшие двух прямых, то эти прямые пересекаются, причем с той стороны от третьей прямой, с какой названная сумма углов будет меньше двух прямых углов.

Слайд 5

И. Ламберт
К. Швейкарт
«Трехсторонник» Швейкарта

Слайд 6

Казанский университет
1826г, Лобачевский представляет Совету Казанского университета «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных»

Слайд 7

В. Буняковский
М. Остроградский

Слайд 8

Гаусс
Труды Н.И. Лобачевского

Слайд 9

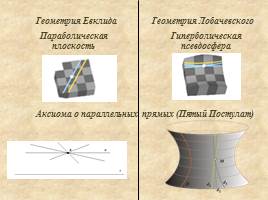
Геометрия Евклида
Геометрия Лобачевского
Аксиома о параллельных прямых (Пятый Постулат)
Параболическая плоскость
Гиперболическая псевдосфера

Слайд 10

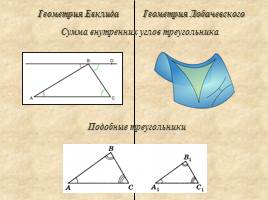
Геометрия Евклида
Геометрия Лобачевского
Сумма внутренних углов треугольника
Подобные треугольники

Слайд 11

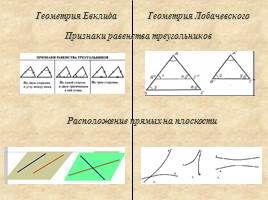
Геометрия Евклида
Геометрия Лобачевского
Признаки равенства треугольников
Расположение прямых на плоскости

Слайд 12

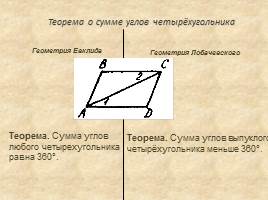
Теорема о сумме углов четырёхугольника
Теорема. Сумма углов любого четырехугольника равна 360°.
Теорема. Сумма углов выпуклого четырёхугольника меньше 360°.
Геометрия Евклида
Геометрия Лобачевского

Слайд 13

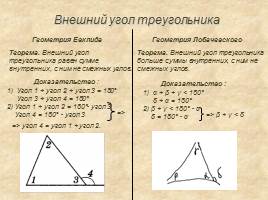
Внешний угол треугольника
Геометрия Евклида
Геометрия Лобачевского
Угол 1 + угол 2 + угол 3 = 180° Угол 3 + угол 4 = 180° 2) Угол 1 + угол 2 = 180°- угол 3 Угол 4 = 180° - угол 3
=>
=> угол 4 = угол 1 + угол 2.
α + β + γ < 180° δ + α = 180° 2) β + γ < 180° - α δ = 180° - α
=> β + γ < δ
Теорема. Внешний угол треугольника равен сумме внутренних, с ним не смежных углов.
Доказательство :
Доказательство :
Теорема. Внешний угол треугольника больше суммы внутренних, с ним не смежных углов.

Слайд 14

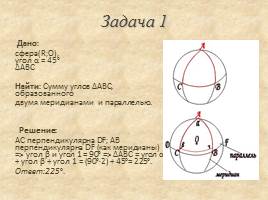
Задача 1
Дано: сфера(R;О), угол α = 45°  ΔABC Найти: Сумму углов ΔABC, образованного двумя меридианами и параллелью. Решение: AC перпендикулярна DF; AB перпендикулярна DF (как меридианы) => угол β и угол 1 = 90° => ΔABC = угол α + угол β + угол 1 = (90°·2) + 45°= 225°. Ответ:225°.

Слайд 15

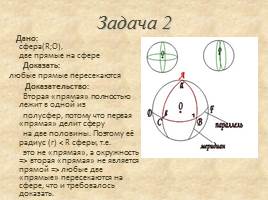
Задача 2
Дано: сфера(R;О), две прямые на сфере Доказать: любые прямые пересекаются Доказательство: Вторая «прямая» полностью лежит в одной из полусфер, потому что первая «прямая» делит сферу на две половины. Поэтому её радиус (r) < R сферы, т.е. это не «прямая», а окружность => вторая «прямая» не является прямой => любые две «прямые» пересекаются на сфере, что и требовалось доказать.

Слайд 16

Заключение
В нашей исследовательской работе цель была достигнута, так как были решены все поставленные задачи. В описании данной работы мы выяснили различия геометрий двух величайших математиков. Содержащиеся в работе сведения дают нам возможность для рассмотрения её в дальнейшем её практического применения. Исследование расширило наши знания о нескольких математиках, а также в корне изменило наше мнение относительно геометрии, изучаемой в школе.

Слайд 17

Слайд 18

Спасибо за внимание!