Презентация - Урок геометрии "Перпендикулярные прямые"
просмотров
Текст этой презентации
Слайд 1
Перпендикулярные прямые
Слайд 2
Сегодня на уроке мы с вами узнаем: Какие углы называются смежными и вертикальными; познакомимся с их свойствами;
Какие прямые называются перпендикулярными;
Будем учиться решать задачи, используя эти свойства.
Слайд 3
Слайд 4
А
В
С
М
В
С
О
D
А
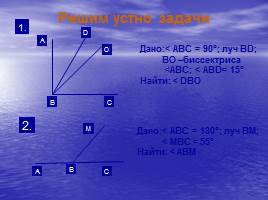
Дано:< АВС = 90°; луч ВD; ВО –биссектриса <АВС; < АВD= 15°
Найти: < DВО
Дано:< АВС = 180°; луч ВМ; < МВС = 55°
Найти: < АВМ
Решим устно задачи
1.
2.
Слайд 5
Задание №1.
Р
D
Е
С
80°
Как называется угол РDЕ?
Чему равна его градусная мера?
Из скольких углов состоит угол РDЕ? Назовите эти углы. Запишите математическую взаимосвязь и, используя ее, вычислите угол РDС.
< РDС + < CDE = 1800
Изобразите с помощью транспортира угол СDЕ = 80°. Проведите прямую DЕ и отметьте на ней точку Р так, чтобы точка D лежала между точками Р и Е.
Слайд 6
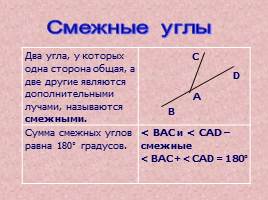
Смежные углы
Два угла, у которых одна сторона общая, а две другие являются дополнительными лучами, называются смежными.
Сумма смежных углов равна 180° градусов. < BAC и < CAD – смежные
< BAC + < CAD = 180°
В
D
А
С
Слайд 7
Сумма смежных углов равна 180
Дано: < BAC и < CAD – …
Доказать: < BAC + < CAD =…
Доказательство:
< BAD = < . . . + < . . .
< BAD – развернутый, значит, < BAD = . . . , следовательно, < BAC + < CAD =….
Что и требовалось доказать.
Слайд 8
По рисунку вычислите:
а) < BAC, если < CАD = 123°.
б) < CАD, если Если один из смежных углов равен 90° градусов, то и другой угол равен 90° градусов.
Слайд 9
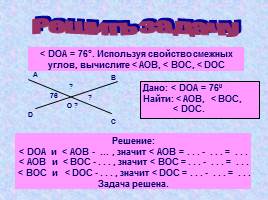
Решить задачу
< DОА = 76°. Используя свойство смежных углов, вычислите < АОB, < BОC, < DОC
А
В
С
D
76
?
О ?
?
Дано: < DОА = 760
Найти: < АОB, < BОC, < DОC.
Решение:
< DОА и < АОB - … , значит < АОB = . . . - . . . = . . .
< АОB и < BОC - . . . , значит < BОC = . . . - . . . = . . .
< BОC и < DОC - . . . , значит < DОC = . . . - . . . = . . .
Задача решена.
Слайд 10
Вертикальные углы
Два угла, стороны одного из которых являются дополнительными лучами сторон другого, называются вертикальными.
Вертикальные углы равны. < 1 и < 2 – вертикальные
< 3 и < 4 – вертикальные < 1 = < 2 < 3 = < 4
Слайд 11
Докажем, что вертикальные углы равны, заполняя следующие записи.
Дано: < 1 и < 2 – вертикальные
Доказать: < 1 = < 2
Доказательство:
Что и требовалось доказать.
< 1 и < 3 - . . ., значит, из сумма равна . . ., тогда < 1 = . . . - . . .
< 2 и < 3 тоже . . . , значит < 2 = . . . - . . .
Так как < 1 = . . . - . . . и < 2 = . . . - . . . , то . . . = . . . .
Слайд 12
Задание 2.
< 1 и < 2 – вертикальные. а) < 1 + < 2 = 100°; б) < 1 + < 2 = 180° . Найдите < 1 и < 2 .
Две пересекающиеся прямые называются перпендикулярными, если они образуют
четыре прямых угла.
Перпендикулярность прямых АС и ВD обозначается так: АС ┴ ВD.
1
2
а)
б)
Слайд 13
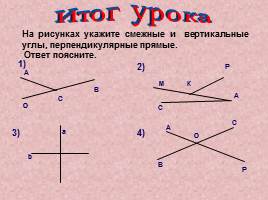
Итог урока
На рисунках укажите смежные и вертикальные углы, перпендикулярные прямые. Ответ поясните.
А
В
С
О
1)
2)
М
Р
А
К
С
3)
а
b
4)
А
О
С
В
Р
Слайд 14
Задание на дом
I уровень: № 55, №58 (а);
II уровень: №56, № 61 (а).
П. 11, 12.
Выучить формулировки определения и свойства вертикальных и смежных углов, перпендикулярных прямых.
Уметь доказывать свойства смежных и вертикальных углов.
Желаю успехов!
Похожие презентации
Обобщающий урок «Перпендикулярность прямых и плоскостей»
Перпендикулярные прямые
Вводный урок по Геометрии «Знакомьтесь - Геометрия»
Обобщающий урок по теме «Параллельные
прямые»
Параллельные прямые
Поделиться ссылкой на презентацию через:
Код для вставки видеоплеера презентации на свой сайт: