Текст этой презентации
Слайд 1

Полуправильный многогранник�
Выполнили ученики 9 «Е» класса:
Грачёв Д.
Ракитов Д.
Удалова Л.
Слайд 2

Цели проекта:
Подробнее изучить тему «Полуправильные многогранники»
Ознакомиться с понятием «Полуправильные многогранники» Рассмотреть каждый из видов этих многогранников
Обобщить полученные знания по теме
Слайд 3

Полуправильные многогранники — это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки
Определение включает в себя различные типы многогранников, сюда относятся архимедовы тела (впервые полуправильные многогранники были открыты Архимедом) и каталановы тела
Слайд 4
Полуправильными называются тела, у которых отсутствует только одно из первых двух свойств правильных тел:
1) Все грани являются правильными многоугольниками;
2) Все грани одинаковы;
3) Тело относится к одному из трёх существующих типов пространственной симметрии.
Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел.
Слайд 5
Группы архимедовых тел
Первую из них составляют пять многогранников, которые получаются из платоновых тел в результате их усечения:
1) Усечённый куб
2) Усечённый октаэдр
3) Усечённый икосаэдр
4) Усечённый тетраэдр
5) Усечённый додекаэдр
Слайд 6
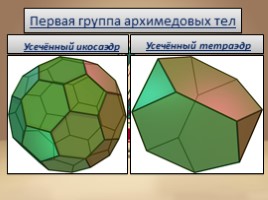
Первая группа архимедовых тел
Усечённый икосаэдр
Усечённый тетраэдр
Слайд 7
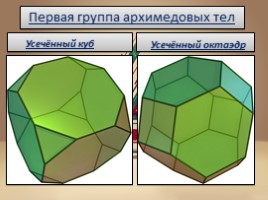
Первая группа архимедовых тел
Усечённый куб
Усечённый октаэдр
Слайд 8
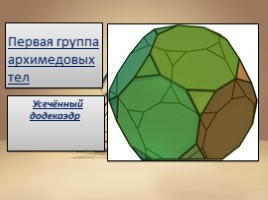
Первая группа архимедовых тел
Усечённый додекаэдр
Слайд 9
Группы архимедовых тел
Вторую группу архимедовых тел составляют два тела:
1) Кубооктаэдр
2) Икосододекаэдр
Слайд 10

Вторая группа архимедовых тел
Кубооктаэдр
Икосододекаэдр
Слайд 11

Группы архимедовых тел
В третью группу входят два многогранника:
1) Ромбокубооктаэдр
2) Ромбоикосододекаэдр
Слайд 12
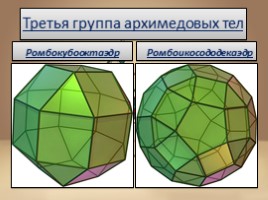
Третья группа архимедовых тел
Ромбокубооктаэдр
Ромбоикосододекаэдр
Слайд 13

Группы архимедовых тел
Четвёртую группу тел составляют многогранники, которые получаются при последовательном срезании каждой из вершин:
1) Курносый куб
2) Курносый додекаэдр
Слайд 14
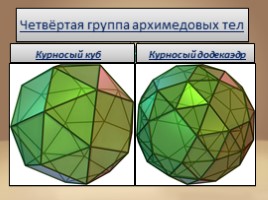
Четвёртая группа архимедовых тел
Курносый куб
Курносый додекаэдр
Слайд 15

Каталановы тела
Каталановы тела имеют конгруэнтные грани (переводимые друг в друга сдвигом, вращением или отражением), равные двугранные углы и правильные многогранные углы.
Слайд 16
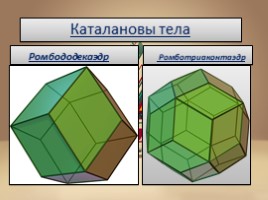
Каталановы тела
Ромбододекаэдр
Ромботриаконтаэдр
Слайд 17
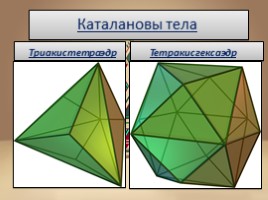
Каталановы тела
Триакистетраэдр
Тетракисгексаэдр
Слайд 18
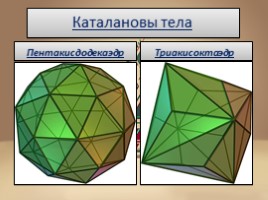
Каталановы тела
Пентакисдодекаэдр
Триакисоктаэдр
Слайд 19
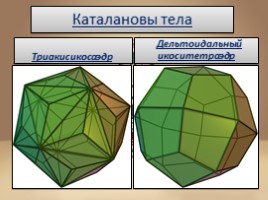
Каталановы тела
Триакисикосаэдр
Дельтоидальный икоситетраэдр
Слайд 20
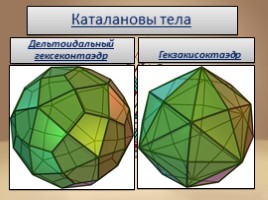
Каталановы тела
Дельтоидальный гексеконтаэдр
Гекзакисоктаэдр
Слайд 21
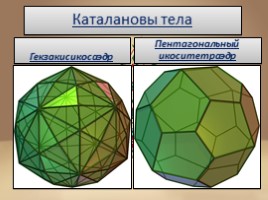
Каталановы тела
Гекзакисикосаэдр
Пентагональный икоситетраэдр
Слайд 22

Каталановы тела
Пентагональный гексеконтаэдр
Слайд 23

Слайд 24
Литература/Ресурсы
http://http-wikipediya.ru/wiki/Полуправильный_многогранник
http://bigslide.ru/matematika/40426-polupravilnie-mnogogranniki.html
 Исследовательский проект «Мой рост и мой вес в раздичных единицах измерения»
Исследовательский проект «Мой рост и мой вес в раздичных единицах измерения»
 Упражнения по планиметрии на готовых чертежах 7-8 класс
Упражнения по планиметрии на готовых чертежах 7-8 класс
 Викторина для 7 класса «Начальные геометрические сведения»
Викторина для 7 класса «Начальные геометрические сведения»
 Проверочные работы по геометрии 7 класс
Проверочные работы по геометрии 7 класс
 Многогранники вокруг нас
Многогранники вокруг нас

























