Презентация - Правильные и полуправильные многогранники (9 класс)

Слайд 1

Нальчик 2018г.
«Правильные и полуправильные многогранники» Подготовил : Богатырев А. – ученик 9 класса Руководитель : Архестова М.С.. - учитель ШИ №1

Слайд 2

Цель работы
Понятие многогранников; Виды многогранников ; Правильные многогранники; Полуправильные многогранники;

Слайд 3

Учение о правильных многогранниках изложил в своих трудах Платон. С тех пор правильные многогранники называют Платоновыми телами. Существует пять видов правильных многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр.
Платон
Из истории

Слайд 4

Впервые полуправильные многогранники открыл Архимед. Эти многогранники им подробно описаны, которые позже в честь великого ученого были названы телами Архимеда. Это усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый) куб, "плосконосый" (курносый) додекаэдр.
Архимед

Слайд 5

Многогранник- это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Вспомним
Многогранники
Правильные
Полуправильные

Слайд 6

Правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны. Правильные многогранники еще называют Платоновыми телами. Существует пять правильных многогранников: 1)тетраэдр, 2)куб, 3)октаэдр, 4)икосаэдр, 5)додекаэдр.

Слайд 7

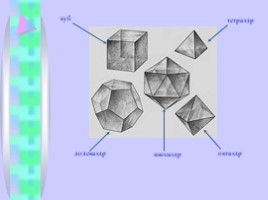
куб
тетраэдр
октаэдр
икосаэдр
додекаэдр

Слайд 8

Полуправильным многогранником называется многогранник, у которого все его многогранные углы равны между собой (но не обязательно правильные), а все его грани- правильные многоугольники (но не все равны между собой). Полуправильные многогранники еще называют архимедовыми телами. Множество Архимедовых тел можно разбить на пять групп.

Слайд 9

Первую из них составляют пять многогранников, которые получаются из Платоновых тел в результате их усечения.
Усеченный куб
Усеченный тетраэдр
Усеченный октаэдр
Усеченный икосаэдр
Усеченный додекаэдр

Слайд 10

Вторую группу Архимедовых тел составляют два тела, именуемых квазиправильными многогранниками.
кубооктаэдр
икосододекаэдр

Слайд 11

Третья группа Архимедовых тел, в нее входят:
ромбокубооктаэдр
ромбоикосододэкаэдр

Слайд 12

Четвертая группа Архимедовых тел:
курносый куб
курносый додекаэдр

Слайд 13

Пятая группа Архимедовых тел состоит из одного многогранника:
Псевдоромбокубооктаэдр

Слайд 14

Выводы
В данной работе были изучены понятия многогранника, правильных и полуправильных многогранников, группы Арихимедовых тел. Цели работы были достигнуты

Слайд 15

Литература
1. В.А. Гусев, Ю.М. Колякин, Г.Н. Луканин « Векторы в школьном курсе геометрии» 2. В.Г. Болтянский «Векторы в курсе высшей математики» 3. В.А. Гусев, А.Г. Мордкович «Справочные материалы: математика»

Слайд 16

Спасибо за внимание