Презентация - Решение задач с помощью уравнений

Слайд 1

Решение задач с помощью
уравнений

Слайд 2

Научиться решать задачи с помощью целых и дробных уравнений с составлением таблицы.
Цель:

Слайд 3

Один из основных принципов алгебраических решений, это то, что величина должна присутствовать в уравнении. Это позволит нам записать условия так, как если бы задача уже была решена. После этого, останется лишь решить уравнение и найти общее значение всех известных величин. Так как эти величины равны неизвестной величине на другой стороне уравнения, то величина всех известных значений будет означать, что задача решена.

Слайд 4

Этапы решения задачи
Этапы решения задачи
Первый этап. Составление математической модели. Вводится переменная, текст задачи переводится на математический язык, составляется уравнение.
Второй этап. Работа с математической моделью. Решение уравнения.
Третий этап. Ответ на вопрос задачи. Анализируя полученное решение, записывается ответ на вопрос задачи.

Слайд 5

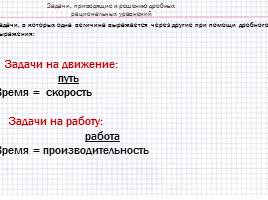
Задачи, приводящие к решению дробных рациональных уравнений
Задачи, в которых одна величина выражается через другие при помощи дробного выражения: Задачи на движение: путь Время = скорость Задачи на работу: работа Время = производительность

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Пусть км/ч - скорость автобуса, тогда составим и заполним таблицу: Т.к. по условию задачи пассажир опоздал на автобус на 10 минут =часа, то составим и решим уравнение: 720(х+10) - 720х= х (х+10), х2+10х-7200=0, Далее решая квадратное уравнение, получаем: х1=80, х2=-90, -90 - не входит в ОДЗ, значит, скорость автобуса равна 80 км/ч. Ответ: 80км/ч.
Автобус-экспресс отправился от вокзала в аэропорт, находящийся на расстоянии 120км от вокзала. Пассажир, опоздавший на 10 минут на автобус, решил добраться до аэропорта на такси. Скорость такси на 10км/ч больше скорости автобуса. С какой скорость ехал автобус, если он приехал в аэропорт одновременно с такси?

Слайд 10

Пусть х литров воды в минуту пропускает первая труба Составим и решим уравнение 48х+192-48х-2х^2-8х=0 -2х^2-8х+192=0 Х1=8 Х2=-12 – не удовл. условие задачи Ответ: 8 литров.
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая труба. Сколько литров в минуту пропускает первая труба, если резервуар объёмом 48 литров она заполняет на 2 минуты дольше, чем вторая труба?

Слайд 11

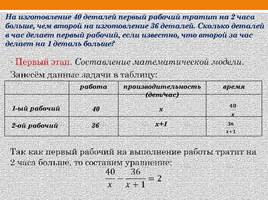
Слайд 12

Слайд 13

Слайд 14

Поезд опаздывал на 1 час,чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию. Пусть х км/ч – скорость по расписанию Составим и решим уравнение: = 1
720х+7200-720х-х2-10х=0 х 2 +10х-7200=0 Х1=80 х2= -90 (не удовлетворяет условию задачи). 80 км/час- скорость поезда по расписанию. Ответ: 80 км/час.

Слайд 15

Слайд 16

D=32400 x1=-100 – не удов. условие задачи x2=80 – скорость товарного поезда Значит 80+20=100 – скорость скорого поезда. Ответ: 80 км/ч, 100 км/ч.

Слайд 17

Итог: Чтобы решать задачи с помощью уравнений необходимо: во-первых, записать условие задачи алгебраическим языком, т.е. таким образом, чтобы получить уравнение; во-вторых, упростить это уравнение до такого вида, в котором неизвестная величина будет стоять с одной стороны, а все известные величины - на противоположной стороне.

Слайд 18

Сухановой Юлии 9а
Конец