Презентация - Гипербола и её свойства

Слайд 1

ГИПЕРБОЛА И ЕЁ СВОЙСТВА

Слайд 2

Гипербола
ОПРЕДЕЛЕНИЕ. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек плоскости F1 и F2 есть величина постоянная и равная 2a (2a < |F1F2|). Точки F1 и F2 называют фокусами гиперболы. Выберем декартову прямоугольную систему координат так, чтобы фокусы F1 и F2 лежали на оси Ox на одинаковом расстоянии от O.
В такой системе координат: F1(–c;0) и F2(c;0) , где |OF1| = |OF2| = c.

Слайд 3

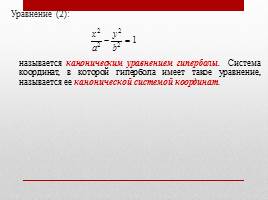
Уравнение (2):
называется каноническим уравнением гиперболы. Система координат, в которой гипербола имеет такое уравнение, называется ее канонической системой координат.

Слайд 4

СВОЙСТВА ГИПЕРБОЛЫ 1) Точек гиперболы нет в полосе, ограниченной прямыми x=a. 2) Гипербола имеет центр симметрии (начало координат) и две оси симметрии (оси Ox и Oy). Центр симметрии гиперболы называют центром гиперболы. Ось симметрии гиперболы, проходящую через фокусы (ось Ox) называют действительной (или фокальной) осью симметрии, а вторую ось (ось Oy) – мнимой осью. 3) Из уравнения гиперболы получаем:

Слайд 5

Прямая ℓ называется асимптотой кривой, если расстояние от точки M кривой до прямой ℓ стремится к нулю при удалении точки M от начала координат. Существуют два вида асимптот – вертикальные и наклонные. Вертикальные асимптоты кривая y=f(x) имеет в тех точках разрыва II рода функции y=f(x) , в которых хотя бы один из односторонних пределов функции равен бесконечности. Наклонные асимптоты кривой y=f(x) имеют уравнение y=k1,2x+b1,2 , где

Слайд 6

Слайд 7

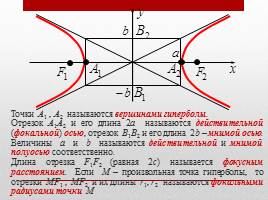
Точки A1 , A2 называются вершинами гиперболы. Отрезок A1A2 и его длина 2a называются действительной (фокальной) осью, отрезок B1B2 и его длина 2b – мнимой осью. Величины a и b называются действительной и мнимой полуосью соответственно. Длина отрезка F1F2 (равная 2c) называется фокусным расстоянием. Если M – произвольная точка гиперболы, то отрезки MF1 , MF2 и их длины r1, r2 называются фокальными радиусами точки M

Слайд 8

ОПРЕДЕЛЕНИЕ. Величина  , равная отношению фокусного расстояния гиперболы к ее действительной оси, называется эксцентриситетом гиперболы, т.е.
Величина  характеризует форму гиперболы. Зная эксцентриситет гиперболы легко найти фокальные радиусы точки M(x;y). Если точка M лежит на правой ветке гиперболы (т.е. x > 0), то
Если M лежит на левой ветке гиперболы (т.е. x < 0), то

Слайд 9

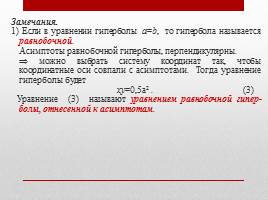
Замечания. 1) Если в уравнении гиперболы a=b, то гипербола называется равнобочной. Асимптоты равнобочной гиперболы, перпендикулярны.  можно выбрать систему координат так, чтобы координатные оси совпали с асимптотами. Тогда уравнение гиперболы будет xy=0,5a2 . (3) Уравнение (3) называют уравнением равнобочной гипер-болы, отнесенной к асимптотам.

Слайд 10

2) Если выбрать систему координат так, чтобы фокусы F1 и F2 были на одинаковом расстоянии от O(0;0), но лежали на Oy, то уравнение гиперболы будет иметь вид
Для этой гиперболы: действительная ось – ось Oy, мнимая ось – ось Ox, F1(0;–c) и F2 (0;c) (где )
асимптоты:
фокальные радиусы точки M(x;y) находятся по формулам

Слайд 11

СПАСИБО ЗАВНИМАНИЕ !!!