Презентация - Степенная функция её свойства и график

Слайд 1

Степенная функция
Её свойства и график
_____ _______ ______ ________ _____

Слайд 2

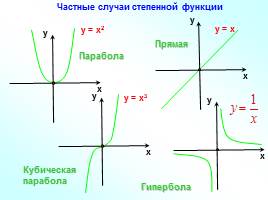
у = х2
у = х3
Парабола
Кубическая парабола
Гипербола
у = х
Прямая
Частные случаи степенной функции

Слайд 3

Функция вида у = хр, где р – действительное число называется степенной функцией
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень

Слайд 4

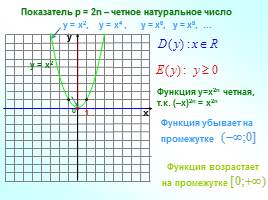
Показатель р = 2n – четное натуральное число
1
0
х
у
у = х2, у = х4 , у = х6, у = х8, …
у = х2
Функция у=х2n четная, т.к. (–х)2n = х2n

Слайд 5

y
x
-1 0 1
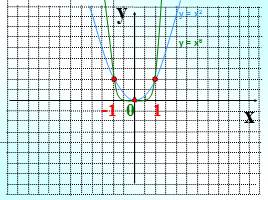
у = х2
у = х6

Слайд 6

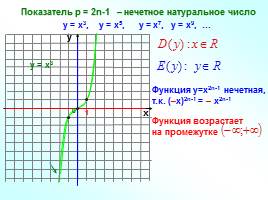
Показатель р = 2n-1 – нечетное натуральное число
1
х
у
у = х3, у = х5, у = х7, у = х9, …
у = х3
Функция у=х2n-1 нечетная, т.к. (–х)2n-1 = – х2n-1
0

Слайд 7

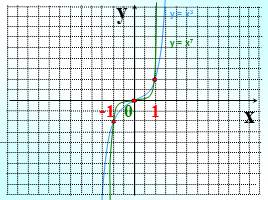
y
x
-1 0 1
у = х3
у = х7

Слайд 8

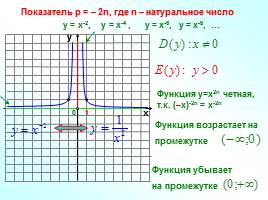
Показатель р = – 2n, где n – натуральное число
1
0
х
у
у = х-2, у = х-4 , у = х-6, у = х-8, …
Функция у=х2n четная, т.к. (–х)-2n = х-2n

Слайд 9

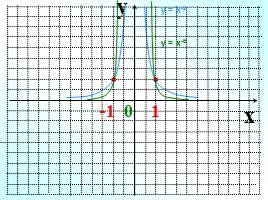
y
x
-1 0 1
у = х-2
у = х-6

Слайд 10

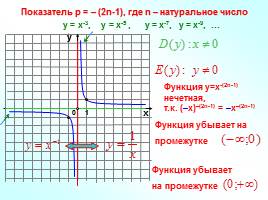
Показатель р = – (2n-1), где n – натуральное число
1
0
х
у
у = х-3, у = х-5 , у = х-7, у = х-9, …
Функция у=х-(2n-1) нечетная, т.к. (–х)–(2n-1) = –х–(2n-1)

Слайд 11

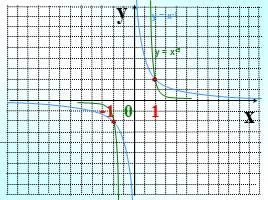
y
x
-1 0 1
у = х-1
у = х-5

Слайд 12

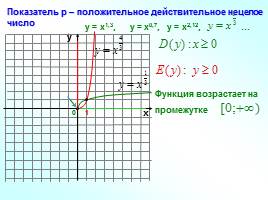
0
Показатель р – положительное действительное нецелое число
1
х
у
у = х1,3, у = х0,7, у = х2,12, …

Слайд 13

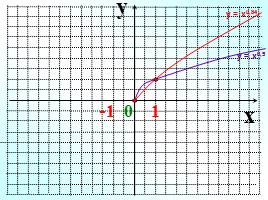
y
x
-1 0 1
у = х0,5

Слайд 14

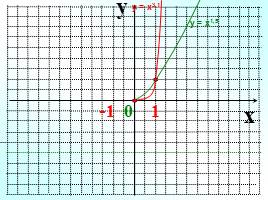
y
x
-1 0 1

Слайд 15

0
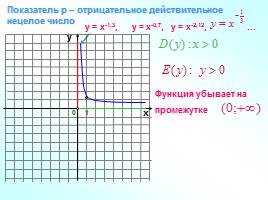
Показатель р – отрицательное действительное нецелое число
1
х
у
у = х-1,3, у = х-0,7, у = х-2,12, …

Слайд 16

y
x
-1 0 1

Слайд 17

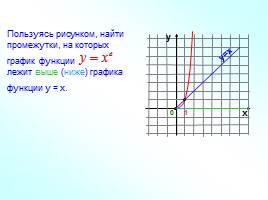
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
0
1
х
у
у=х

Слайд 18

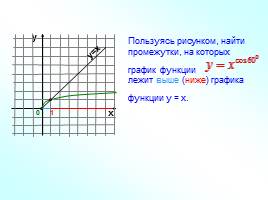
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
у
0
1
х
у=х

Слайд 19

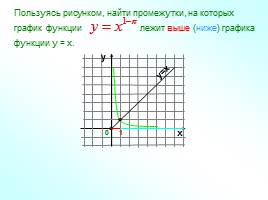
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.

Слайд 20

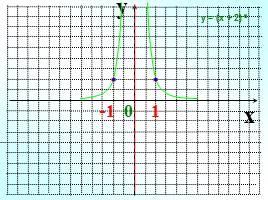
y
x
-1 0 1
у = (х + 2)-6

Слайд 21

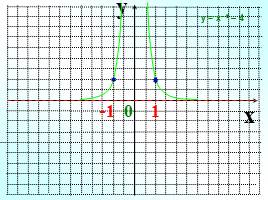
y
x
-1 0 1
у = х– 6 – 4

Слайд 22

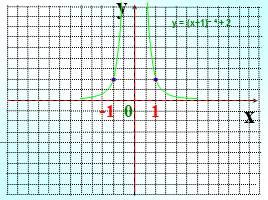
y
x
-1 0 1
у = (х+1)– 4 + 2

Слайд 23

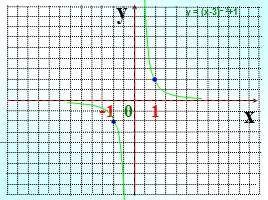
y
x
-1 0 1
у = (х-3)– 3+1

Слайд 24

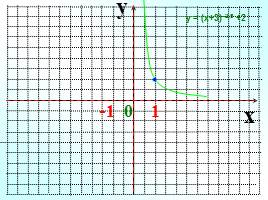
y
x
-1 0 1
у = (х+3)–2,5 +2