Презентация - Площади фигур

Слайд 1

Презентация на тему: Площади фигур
Выполнила ученица: 9 класса А Воронина Анастасия Алексеевной Учителю: Игуменовой Нине Васильевне
Цель работы : в своей работе я хочу показать вам как решать задачи с площадями фигур , такими фигурами как « Квадрат , Прямоугольник , Прямоугольный треугольник, Равнобедренный треугольник, Трапеция , Треугольники общего вида , Параллелограмм, Ромб ,Окружность.»

Слайд 2

Задание № 11 Квадрат— правильный четырёхугольник , то есть четырёхугольник, у которого все углы и стороны равны.
Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.
Ре­ше­ние. Пло­щадь по­лу­чив­шей­ся фи­гу­ры равна раз­но­сти пло­ща­дей квад­ра­та и пря­мо­уголь­ни­ка: 6 · 6 − 4 · 2 = 28.   Ответ: 28

Слайд 3

Прямоугольник — четырёхугольник , у которого все углы прямые (равны 90 градусам).
Задание № 11
В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сто­ро­на равна 12. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.
Ре­ше­ние . Пло­щадь пря­мо­уголь­ни­ка равна про­из­ве­де­нию его смеж­ных сто­рон, по­это­му она равна 120.   Ответ: 120.

Слайд 4

Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)
Задание № 11
Решение Угол 45 град. => второй угол тоже 45 град. => треугольник равнобедренный с катетами по 10 => S = 1/2 * 10 * 10 = 50
В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 4, а ост­рый угол, при­ле­жа­щий к нему, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.
Ответ: 50

Слайд 5

Задание № 11
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине
Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 16, а бо­ко­вая сто­ро­на — 5. Най­ди­те пло­щадь тре­уголь­ни­ка.
Решение Р треугольника=a+2b S треугольника=√р(р-a)(p-b)(p-c) P=a+b+c/2       a=16-5*2=6 p=16/2=8 S треугольника=√8(8-5)(8-5)(8-6)=√144=12
Ответ:12

Слайд 6

Задание № 11
Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.
Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.
Решение Из рисунка AB = 11, CD = 5, DH = 5. S = (AB+CD)*DH/2 = (11+5)*5/2 = 40. Площадь трапеции равна 40.   Ответ: 40.

Слайд 7

Задание № 11
Треугольник общего вида  – простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками и тремя отрезками, попарно соединяющими эти точки
Сто­ро­на тре­уголь­ни­ка равна 12, а вы­со­та, про­ведённая к этой сто­ро­не, равна 33. Най­ди­те пло­щадь этого тре­уголь­ни­ка.
Ре­ше­ние. Пло­щадь тре­уголь­ни­ка равна по­лу­про­из­ве­де­нию сто­ро­ны тре­уголь­ни­ка на вы­со­ту, про­ве­ден­ную к этой сто­ро­не: Ответ: 216
Ре­ше­ние. Пло­щадь тре­уголь­ни­ка равна по­лу­про­из­ве­де­нию сто­ро­ны тре­уголь­ни­ка на вы­со­ту, про­ве­ден­ную к этой сто­ро­не: S=1/2*16*27=216 Ответ: 216

Слайд 8

Задание № 11
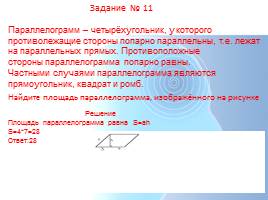
Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Противоположные стороны параллелограмма попарно равны. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Решение Площадь параллелограмма равна  S=ah S=4*7=28 Ответ:28
Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке

Слайд 9

Задание № 11
Ромб – четырёхугольник, у которого все стороны равны между собой. У ромба есть две диагонали, соединяющие несмежные вершины. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Найти сторону и площадь ромба, если его диагонали равны 10 см и 24 см. Решение. Sромба = 1/2 · АС · ВD = 240/2 = 120 (см2). АС2 + ВD2 = 2(АВ2 + ВС2) (по свойству сторон и диагоналей ромба), поэтому 100 + 576 = 4 · АВ2; АВ2 = 169; АВ = 13 см. АВ = ВС = СD = АD = 13 см. Sромба = 120 см2. Ответ: АВ = 13 см, S = 120 см2.

Слайд 10

Задание № 11
Окружность. • Вписанный угол равен половине дуги, на которую он опирается; • Угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними. • Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. • Отрезки касательных прямых к окружности равны. • Пусть через точку А проведена касательная АВ к окружности (В – точка касания) и секущая, пересекающая окружность в двух точках Р и Q. Тогда АВ2 = АР ⋅ AQ. • Пусть через точку А проведены секущие к окружности, пересекающие её в точках первая В1 и С1, а другая – В2 и С2. Тогда АВ1 ⋅ АС1 = АВ2⋅АС2. ОПОРНАЯ ЗАДАЧА № 1 Доказательство: ∆АС1В2 ∼ ∆АС2В1 по двум углам: ∠ АС1В2 = ∠ АС2В1 как углы, опирающиеся на дугу В1В2. ∠ С1В1С2 = ∠ С1В2С2 как углы опирающиеся на дугу С1С2, а следовательно равны углы, дополняющие их до 180° , т.е. ∠ АВ2С1 = ∠ А В1С2. Тогда АС1 АС2 = АВ2 АВ1 или АВ1 ·АС1 = АВ2 ·АС2.
Вывод :в своей презентации я вам показала понятия решения задач ОГЭ Спасибо за внимание