Презентация - Пространственные фигуры

Слайд 1

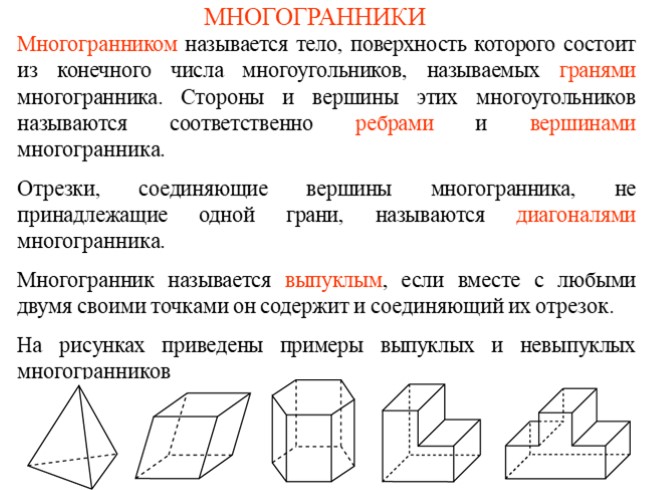
МНОГОГРАННИКИ
Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника. Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями многогранника. Многогранник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок. На рисунках приведены примеры выпуклых и невыпуклых многогранников

Слайд 2

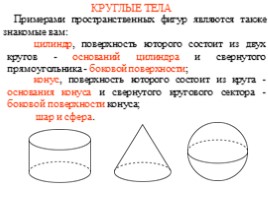
КРУГЛЫЕ ТЕЛА
Примерами пространственных фигур являются также знакомые вам:
шар и сфера.
конус, поверхность которого состоит из круга - основания конуса и свернутого кругового сектора - боковой поверхности конуса;
цилиндр, поверхность которого состоит из двух кругов - оснований цилиндра и свернутого прямоугольника - боковой поверхности;

Слайд 3

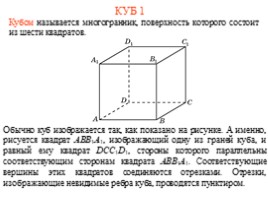
КУБ 1
Кубом называется многогранник, поверхность которого состоит из шести квадратов.
Обычно куб изображается так, как показано на рисунке. А именно, рисуется квадрат ABB1A1, изображающий одну из граней куба, и равный ему квадрат DCC1D1, стороны которого параллельны соответствующим сторонам квадрата ABB1A1. Соответствующие вершины этих квадратов соединяются отрезками. Отрезки, изображающие невидимые ребра куба, проводятся пунктиром.

Слайд 4

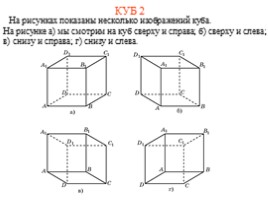
КУБ 2
На рисунках показаны несколько изображений куба.
На рисунке а) мы смотрим на куб сверху и справа; б) сверху и слева; в) снизу и справа; г) снизу и слева.

Слайд 5

Упражнение 1
Изобразите куб на клетчатой бумаге, аналогично данному на рисунке.

Слайд 6

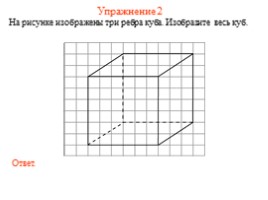
Упражнение 2
На рисунке изображены три ребра куба. Изобразите весь куб.

Слайд 7

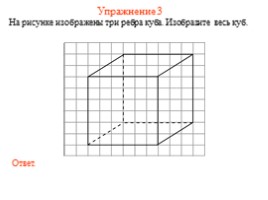
Упражнение 3
На рисунке изображены три ребра куба. Изобразите весь куб.

Слайд 8

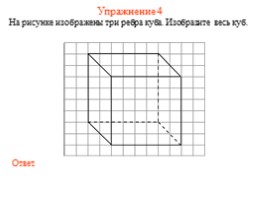
Упражнение 4
На рисунке изображены три ребра куба. Изобразите весь куб.

Слайд 9

Упражнение 5
На рисунке изображены три ребра куба. Изобразите весь куб.

Слайд 10

ПАРАЛЛЕЛЕПИПЕД
Параллелепипедом называется многогранник, поверхность которого состоит из шести параллелограммов.
Прямоугольным параллелепипедом называется параллелепипед, грани которого – прямоугольники.
Обычно параллелепипед изображается так, как показано на рисунке. А именно, рисуется параллелограмм ABB1A1, изображающий одну из граней параллелепипеда, и равный ему параллелограмм DCC1D1, стороны которого параллельны соответствующим сторонам параллелограмма ABB1A1. Соответствующие вершины этих параллелограммов соединяются отрезками. Отрезки, изображающие невидимые ребра куба, проводятся пунктиром. В случае прямоугольного параллелепипеда вместо параллелограммов, изображающих две грани, рисуются равные прямоугольники.

Слайд 11

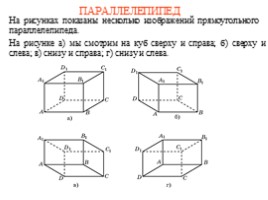
ПАРАЛЛЕЛЕПИПЕД
На рисунках показаны несколько изображений прямоугольного параллелепипеда.
На рисунке а) мы смотрим на куб сверху и справа; б) сверху и слева; в) снизу и справа; г) снизу и слева.

Слайд 12

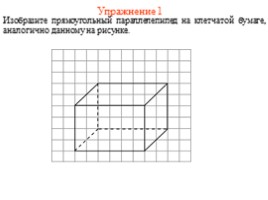
Упражнение 1
Изобразите прямоугольный параллелепипед на клетчатой бумаге, аналогично данному на рисунке.

Слайд 13

Упражнение 2
На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.

Слайд 14

Упражнение 3
На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.

Слайд 15

Упражнение 4
На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.

Слайд 16

Упражнение 5
На рисунке изображены три ребра прямоугольного параллелепипеда. Изобразите весь параллелепипед.

Слайд 17

ПРИЗМА
Призмой называется многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, имеющих общие стороны с каждым из оснований и называемых боковыми гранями призмы. Стороны боковых граней называются боковыми ребрами призмы. Призма называется n-угольной, если ее основаниями являются n-угольники.
На рисунке изображена четырехугольная призма. ABCD и A1B1C1D1 – равные четырехугольники с соответственно параллельными сторонами. Соответствующие вершины этих четырехугольников соединены отрезками. Отрезки, изображающие невидимые ребра призмы, проводятся пунктиром.

Слайд 18

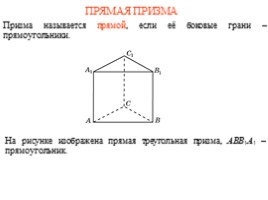
ПРЯМАЯ ПРИЗМА
Призма называется прямой, если её боковые грани – прямоугольники.
На рисунке изображена прямая треугольная призма, ABB1A1 – прямоугольник.

Слайд 19

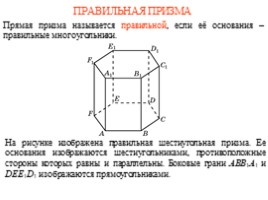
ПРАВИЛЬНАЯ ПРИЗМА
Прямая призма называется правильной, если её основания – правильные многоугольники.
На рисунке изображена правильная шестиугольная призма. Ее основания изображаются шестиугольниками, противоположные стороны которых равны и параллельны. Боковые грани ABB1A1 и DEE1D1 изображаются прямоугольниками.

Слайд 20

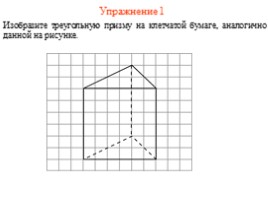
Упражнение 1
Изобразите треугольную призму на клетчатой бумаге, аналогично данной на рисунке.

Слайд 21

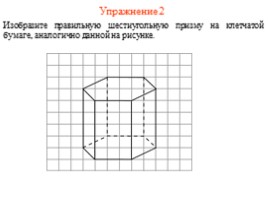
Упражнение 2
Изобразите правильную шестиугольную призму на клетчатой бумаге, аналогично данной на рисунке.

Слайд 22

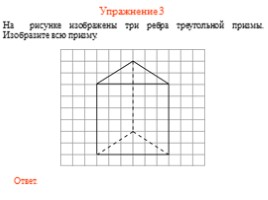
Упражнение 3
На рисунке изображены три ребра треугольной призмы. Изобразите всю призму.

Слайд 23

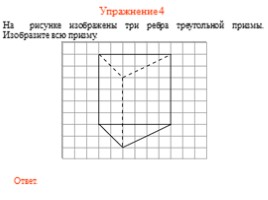
Упражнение 4
На рисунке изображены три ребра треугольной призмы. Изобразите всю призму.

Слайд 24

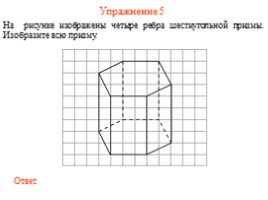
Упражнение 5
На рисунке изображены четыре ребра шестиугольной призмы. Изобразите всю призму.

Слайд 25

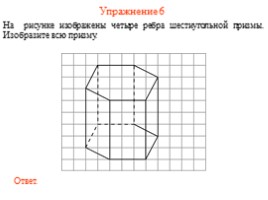
Упражнение 6
На рисунке изображены четыре ребра шестиугольной призмы. Изобразите всю призму.

Слайд 26

Упражнение 7
Существует ли призма, которая имеет:
Ответ: Нет.
а) 4 ребра?
Ответ: Нет.
Ответ: Да.
Ответ: Да.
б) 6 рёбер?
в) 12 рёбер?
г) 21 ребро?

Слайд 27

Упражнение 8
Какой многоугольник лежит в основании призмы, которая имеет:
Ответ: Шестиугольник.
а) 18 рёбер?
б) 24 вершины?
в) 36 граней?
Ответ: Двенадцатиугольник.
Ответ: Тридцатичетырёхугольник.

Слайд 28

ПИРАМИДА
Пирамидой называется многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников с общей вершиной, называемых боковыми гранями пирамиды. Стороны боковых граней называются боковыми ребрами пирамиды. Общая вершина боковых граней называется вершиной пирамиды Пирамида называется n-угольной, если ее основанием является n-угольник.
На рисунке изображена четырехугольная пирамида. Четырехугольник ABCD – основание, S – вершина пирамиды.

Слайд 29

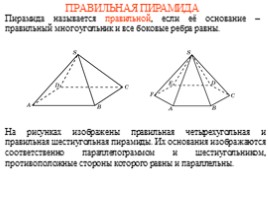
ПРАВИЛЬНАЯ ПИРАМИДА
Пирамида называется правильной, если её основание – правильный многоугольник и все боковые ребра равны.
На рисунках изображены правильная четырехугольная и правильная шестиугольная пирамиды. Их основания изображаются соответственно параллелограммом и шестиугольником, противоположные стороны которого равны и параллельны.

Слайд 30

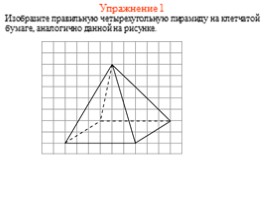
Упражнение 1
Изобразите правильную четырехугольную пирамиду на клетчатой бумаге, аналогично данной на рисунке.

Слайд 31

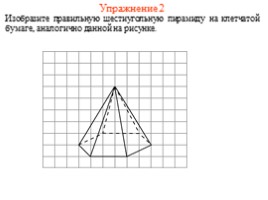
Упражнение 2
Изобразите правильную шестиугольную пирамиду на клетчатой бумаге, аналогично данной на рисунке.

Слайд 32

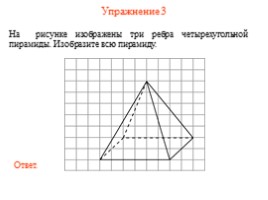
Упражнение 3
На рисунке изображены три ребра четырехугольной пирамиды. Изобразите всю пирамиду.

Слайд 33

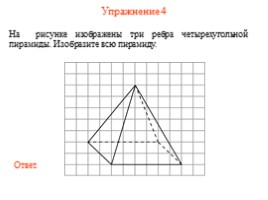
Упражнение 4
На рисунке изображены три ребра четырехугольной пирамиды. Изобразите всю пирамиду.

Слайд 34

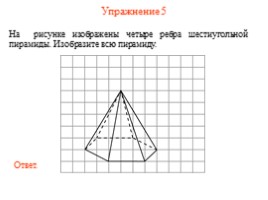
Упражнение 5
На рисунке изображены четыре ребра шестиугольной пирамиды. Изобразите всю пирамиду.

Слайд 35

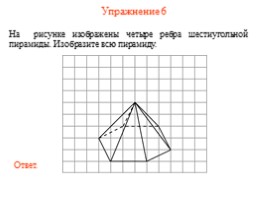
Упражнение 6
На рисунке изображены четыре ребра шестиугольной пирамиды. Изобразите всю пирамиду.

Слайд 36

Упражнение 7
Существует ли пирамида, которая имеет:
а) 10 ребер?
б) 6 рёбер?
в) 24 ребра?
г) 33 ребра?
Ответ: Да.
Ответ: Да.
Ответ: Да.
Ответ: Нет.

Слайд 37

Упражнение 8
Какой многоугольник лежит в основании пирамиды, которая имеет:
Ответ: 59-угольник.
а) 8 рёбер?
б) 22 вершины?
в) 60 граней?
Ответ: 4-угольник.
Ответ: 21-угольник.

Слайд 38

Многогранники 1
У многогранника шесть вершин и в каждой из них сходится четыре ребра. Сколько у него рёбер?

Слайд 39

Многогранники 2
У многогранника двенадцать граней и все они пятиугольные. Сколько у него рёбер?

Слайд 40

Многогранники 3
Сколько рёбер может сходиться в вершине многогранника?
Ответ: Любое число, не меньшее 3.

Слайд 41

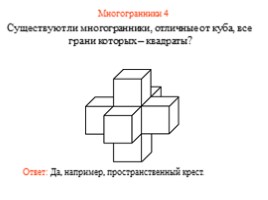
Многогранники 4
Существуют ли многогранники, отличные от куба, все грани которых – квадраты?

Слайд 42

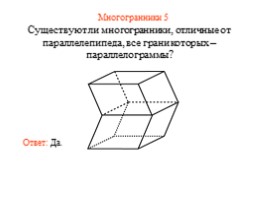
Многогранники 5
Существуют ли многогранники, отличные от параллелепипеда, все грани которых – параллелограммы?

Слайд 43

Многогранники 6
Существуют ли многогранник, у которого:
а) 5 ребер?
Нет.
б) 6 ребер?
Да, тетраэдр.
в) 7 ребер?
Нет.
г) 8 ребер?
Да, четырехугольная пирамида.
д) 9 ребер?
Да, треугольная призма.
е) 10 ребер?
Да, пятиугольная пирамида.
ж)* 11 ребер?
Да, пример такого многогранника изображен на рисунке.

Слайд 44

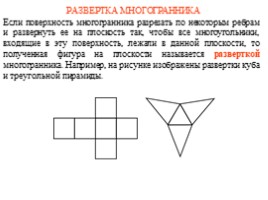
РАЗВЕРТКА МНОГОГРАННИКА
Если поверхность многогранника разрезать по некоторым ребрам и развернуть ее на плоскость так, чтобы все многоугольники, входящие в эту поверхность, лежали в данной плоскости, то полученная фигура на плоскости называется разверткой многогранника. Например, на рисунке изображены развертки куба и треугольной пирамиды.

Слайд 45

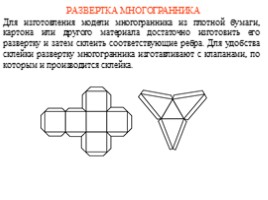
РАЗВЕРТКА МНОГОГРАННИКА
Для изготовления модели многогранника из плотной бумаги, картона или другого материала достаточно изготовить его развертку и затем склеить соответствующие ребра. Для удобства склейки развертку многогранника изготавливают с клапанами, по которым и производится склейка.

Слайд 46

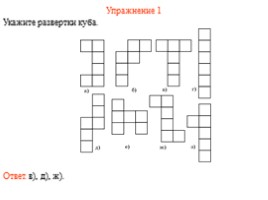
Упражнение 1
Укажите развертки куба.
Ответ. в), д), ж).

Слайд 47

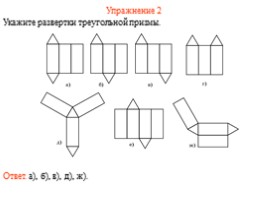
Упражнение 2
Укажите развертки треугольной призмы.
Ответ. а), б), в), д), ж).

Слайд 48

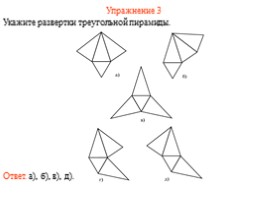
Упражнение 3
Укажите развертки треугольной пирамиды.
Ответ. а), б), в), д).

Слайд 49

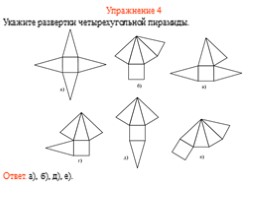
Упражнение 4
Укажите развертки четырехугольной пирамиды.
Ответ. а), б), д), е).