Презентация - Задачи на построение

Слайд 1

Задачи на построение.Строим циркулем и линейкой!
Автор: Наумов Владислав, ученик МОУ «Корниловская СОШ». Учитель : Купцова Е.В., учитель математики МОУ «Корниловская СОШ». п. Двинской Верхнетоемского района Архангельской области

Слайд 2

На данном луче от его начала отложить отрезок, равный данному.
Задача 1

Слайд 3

В
А
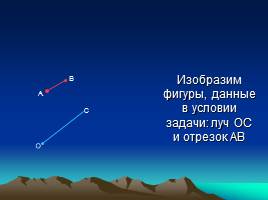
Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ
О
С

Слайд 4

Затем циркулем построим окружность радиуса АВ с центром О. Эта окружность пересечёт луч ОС в некоторой точке D. Отрезок ОD –искомый.
О
С
D

Слайд 5

Задача 2
Отложить от данного луча угол, равный данному.

Слайд 6

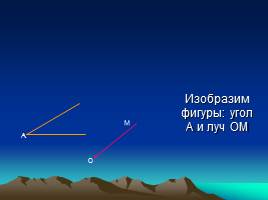
Изобразим фигуры: угол А и луч ОМ
М
О
А

Слайд 7

Проведём окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С.
А
С
В

Слайд 8

Затем проведём окружность того же радиуса с центром в начале данного луча ОМ. Она пересекает луч в точке D.
О
D
М

Слайд 9

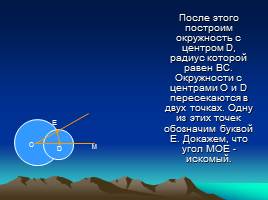
После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ -искомый.
Е
О
D
М

Слайд 10

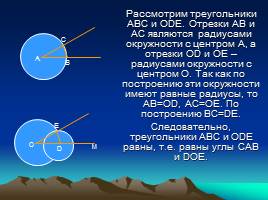
Рассмотрим треугольники АВС и ОDЕ. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки ОD и ОЕ –радиусами окружности с центром О. Так как по построению эти окружности имеют равные радиусы, то АВ=ОD, АС=ОЕ. По построению ВС=DЕ. Следовательно, треугольники АВС и ОDE равны, т.е. равны углы САВ и DOE.
О
Е
D
М
А
С
В

Слайд 11

Задача 3
Построить биссектрису данного угла.

Слайд 12

Нарисуем угол A и проведём окружность (A; r) она пересекает стороны угла в точках В и С.
С
А
В

Слайд 13

Затем проведём две окружности одинакового радиуса ВС с центрами в точках В и С. Они пересекутся в двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е.
С
А
В
Е

Слайд 14

С
А
В
Е
Докажем, что луч АЕ является биссектрисой данного угла ВАС. Рассмотрим треугольники АСЕ и АВЕ. ОНИ равны по трём сторонам. В самом деле, АЕ – общая сторона; АС и АВ равны как радиусы одной и той же окружности; СЕ=ВЕ по построению.

Слайд 15

Дана прямая и точка на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.
Задача 4

Слайд 16

Дана прямая а и дана точка М, принадлежащая этой прямой.
а
М

Слайд 17

На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. Затем построим две окружности с центрами А и В радиуса АВ. Они пересекаются в двух точках: Р и Q.
а
М
А
В
Р
Q

Слайд 18

Проведём прямую QР через точку М, и докажем, что эта прямая – искомая, т. е. что она перпендикулярна к данной прямой а. В самом деле, так как медиана РМ равнобедренного треугольника РАВ является также высотой, то РМ перпендикулярна а.
а
М
А
В
Р
Q

Слайд 19

Задача 5
Построить середину данного отрезка.

Слайд 20

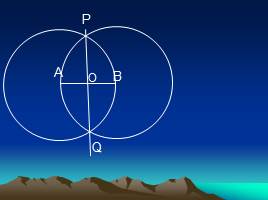
Пусть АВ – данный отрезок. Построим две окружности с центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. Проведём прямую РQ. Точка О пересечения этой прямой с отрезком АВ и есть искомая середина отрезка АВ
О
А
В
Р
Q

Слайд 21

О
А
В
Р
Q

Слайд 22

О
А
В
Р
Q
1
2
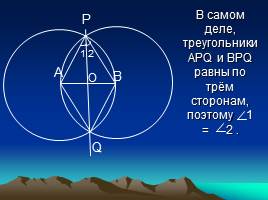
В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому 1 = 2 .

Слайд 23

Следовательно, отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. е. точка О – середина отрезка АВ.