Презентация - Золотое сечение

Слайд 1

Золотое сечение
9 класс

Слайд 2

…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем… Иоганн Кеплер

Слайд 3

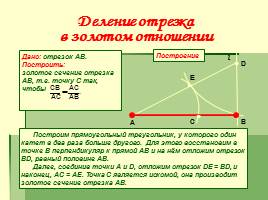
Деление отрезка в золотом отношении
●
●
A
C
B
E
D
Дано: отрезок АВ. Построить: золотое сечение отрезка АВ, т.е. точку С так, чтобы
Построение
l
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нём отложим отрезок BD, равный половине AB. Далее, соединив точки А и D, отложим отрезок DЕ = ВD, и наконец, АС = АЕ. Точка С является искомой, она производит золотое сечение отрезка АВ.
●

Слайд 4

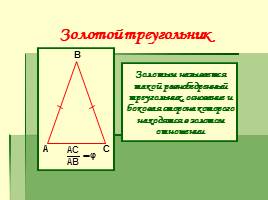
Золотой треугольник
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении.
A
В
С

Слайд 5

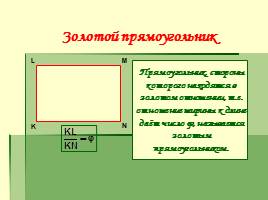
Золотой прямоугольник
Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение ширины к длине даёт число φ, называется золотым прямоугольником.
K
L
M
N

Слайд 6

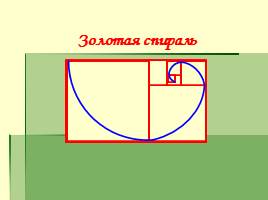
Золотая спираль

Слайд 7

Золотое сечение и золотая спираль в природе

Слайд 8

Слайд 9

Сообщение
Оказывается, что у большинства людей, верхняя точка уха, на рисунке это точка В, делит высоту головы вместе с шеей, т.е. отрезок АС, в золотом отношении. Нижняя точка уха, точка D, делит в золотом отношении расстояние ВС, т.е. расстояние от верхней части уха до основания шеи. Подбородок делит расстояние от нижней точки уха до основания шеи в золотом отношении, т.е. точка Е делит в золотом отношении отрезок DC.

Слайд 10

Аполлон Бельведерский
Измерения нескольких тысяч человеческих тел позволили обнаружить, что пупок делит высоту человека в золотом отношении. Основание шеи делит расстояние от макушки до пупка в золотом отношении. Эти пропорции показаны на изображении знаменитой скульптуры Аполлона Бельведерского. Аполлон считается образцом мужской красоты.

Слайд 11

Работы Фидия
Афина Парфенос
Зевс Олимпийский
Скульптор Фидий часто использовал золотую пропорцию в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского, которая считалась одним из семи чудес света, и статуя Афины Парфенос.

Слайд 12

Фидий руководил строительством храма Парфенон в Афинах. Парфенон – это одно из красивейших произведений древнегреческой архитектуры. Он и сейчас, несмотря на то, что со времени его постройки прошло более 2,5 тысячелетий, производит огромное впечатление. Некогда белоснежный мрамор стал от времени золотисто-розовым. Величественное здание, стоящее на холме из известняка, возвышается над Афинами и их окрестностями.Но поражает оно не своими размерами, а гармоническим совершенством пропорций. Здание не вдавливается своей тяжестью в землю, а как бы парит над нею, кажется очень лёгким. Многие искусствоведы стремились раскрыть секрет того могучего эмоционального воздействия, которое это здание оказывает на зрителя. Разгадку они увидели в том, что в соотношениях многих частей храма присутствует золотая пропорция. Так, отношение высоты здания к его длине равно . Отношения целого ряда частей Парфенона дают число . Говорят «…у греческого храма нет размеров, у него есть пропорции …».
Парфенон

Слайд 13

Домашнее задание
А
В
С
D
E
F
K
M
N
L
1) Произвольный отрезок разделите в золотом отношении. Используя полученные отрезки, постройте золотой треугольник, боковой стороной которого является исходный отрезок. 2) На рисунке изображена пентаграмма. Используя данные обозначения и выполнив необходимые измерения, найдите: а) золотые сечения; б) золотые треугольники.

Слайд 14

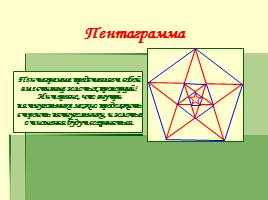
Пентаграмма
Пентаграмма представляет собой вместилище золотых пропорций! Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и золотые отношения будут сохраняться.

Слайд 15

Закон углов
Отсюда получаем уравнение и находим положительный корень Тогда Таким образом, величина среднего углового отклонения ветки соответствует меньшей из двух частей, на которые делится полный угол при золотом сечении.  
В 1850 г. немецкий учёный А. Цейзинг открыл так называемый закон углов, согласно которому средняя величина углового отклонения ветки растения равна примерно 138. Угол между лучами – ветками, обозначим через α, а угол, дополняющий его до 360,  через β. Составим золотую пропорцию деления полного угла, считая, что угол β  большая часть этой величины:

Слайд 16

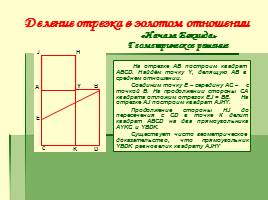
Деление отрезка в золотом отношении
На отрезке АВ построим квадрат АВСD. Найдём точку Y, делящую АВ в среднем отношении. Соединим точку Е – середину АС – с точкой В. На продолжении стороны СА квадрата отложим отрезок ЕJ = ВЕ. На отрезке AJ построим квадрат AJHY. Продолжение стороны HJ до пересечения с CD в точке К делит квадрат ABCD на два прямоугольника AYKC и YBDK. Существует чисто геометрическое доказательство, что прямоугольник YBDK равновелик квадрату AJHY
«Начала Евклида» Геометрическое решение