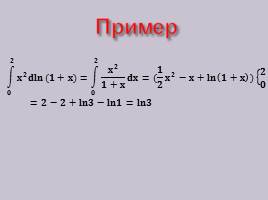Презентация - Обобщение «Интеграл Стилтьеса»

Слайд 1

Интеграл Стилтьеса
Подготовила Студентка ФМг-112 Смолова Диана Александровна

Слайд 2

Применение в теории вероятностей, механике, теории сооружений.

Слайд 3

Интегральная сумма Стилтьеса.
????=???? ???? ???? ???? ???? ???? ???? ???? −???? ???? ????−????
на сегменте [a,b] заданы две ограниченные функции: f(x) и g(x) α= x0 < x1 < x2 < … < xn = b
Эта сумма называется интегральной суммой Стилтьеса

Слайд 4

Интеграл Стилтьеса.
????????????α→0 ????=1 ???? ???? ???? ???? ???? ???? ???? −???? ???? ????−1
???? ???? ???? ???? ???????? ???? .

Слайд 5

Интеграл Стилтьеса
.
???? ???? ???? ???? ???????? ???? .
???? ???? ???? ???? ???? ???? .
Интеграл Римана

Слайд 6

Достаточное условие существования.
f(х) непрерывна на сегменте [а, b] g (х) имеет на этом сегменте ограниченное изменение
интеграл Стилтьеса функции f (х) по функции g (х) на сегменте [a , b] существует.

Слайд 7

Свойства

Слайд 8

Сведение к интегралу Римана
???? ???? ???? ???? ???????? ???? =????????????α→0 ????=1 ???? ???? ???? ???? ???? ???? ???? −???? ???? ????−1 =????????????α→0 ????=1 ???? ???? ???? ???? ???? ???? ???? ???? ???? − ???? ????−1

Слайд 9

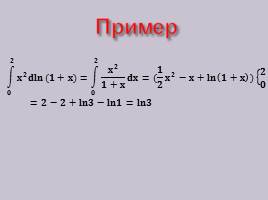
Пример
???? ???? ???? ???? ????????????(????+????)= ???? ???? ???? ???? ????+???? ????????=( ???? ???? ???? ???? −????+ ???????? ????+???? ) ???? ???? =????−????+????????????−????????????=????????????