Презентация - Задания по теме «Разложение многочлена на множители с вынесением общего множителя за скобки»

Слайд 1

Урок алгебры 7 класса Учитель математики высшей категории Белоусова Т.В.
Разложение многочлена на множители вынесением общего множителя за скобки.

Слайд 2

Зачем нам это надо?
Рассмотрим примеры: 3х – 7х + 14х = 10
х(3 – 7 + 14) = 10
10х = 10
1672 – 167*67 =
167(167 – 67) =
167*100 =
16700
Доказать, что (n2 + n) : 2 при любых n.
n(n + 1)
n2 + n =
Возьмем числа 8,9; 17,18; …
т.е в этом произведении всегда есть множитель, который делится на два.
(n2 + n) : 2

Слайд 3

При решении уравнений, в вычислениях бывает удобно заменить многочлен произведением нескольких многочленов. Такое представление называют разложением многочлена на множители.

Слайд 4

Алгоритм отыскания общего множителя нескольких одночленов
1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем. 2. Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени. 3. Произведение коэффициента и переменных найденных на первом и втором шагах, является общим множителем, который надо вынести за скобки.

Слайд 5

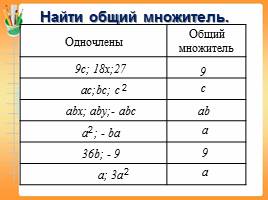
Найти общий множитель.
Одночлены Общий множитель
9c; 18x;27
ac;bc; c
abx; aby;- abc
a ; - ba
36b; - 9
a; 3a
2
2
2
9
с
ab
a
9
a

Слайд 6

Преобразовать многочлен
ax + bx + cx 3x + 3b + 3c 5a – 35bc + 20 mc 3ax - 6bx + 9xc 4a + 8b +16c
2
2
3
= x(a + b + c)
= 3(x + b + c)
= 5 (a - 7bc + 4mc)
= 4 (a + 2b + 4c)

Слайд 7

Правило вынесения общего множителя за скобки
Найти общий множитель у всех членов многочлена; Вынести его за скобки.
После вынесения общего множителя за скобки, в скобках должно остаться столько слагаемых, сколько их было в данном многочлене.

Слайд 8

Разложить на множители:-x4y3-2x3y2+5x2
1. НОД(–1, -2 и 5) = 1. 2. Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2 , так как наименьший показатель степени 2. 3. Переменная y входит не во все члены многочлена, значит, ее нельзя вынести за скобки. Вывод: за скобки можно вынести x2. В данном случае целесообразнее вынести -x2. Получим: -x4y3-2x3y2+5x2
=-x2(x2y3+2xy2-5).

Слайд 9

Разложить на множители многочлен36a6b3 - 96a4b4 + 64a2b5 .
Рассмотрим коэффициенты 36, 192, 64. Все они делятся на 4, причем это наибольший общий делитель, вынесем его за скобки.
Итак, за скобки вынесем 4a2b3. Тогда получим в скобках от первого одночлена 9a4 (36a6b3 :4a2b3) , от второго -48a2b, от третьего 16b2 .
Во все члены многочлена входит переменная a (соответственно a6, a4, a2), поэтому за скобки можно вынести a2. Точно так же во все члены многочлена входит переменная b (соответственно b3, b4, b5) – за скобки можно вынести b3.
36a6b3-192a4b4+64a2b5=4a2b3(9a4 - 48a2b + 16b2)

Слайд 10

Разложить на множители а4x4 + x2a2 + a4
6n3 + 3n2 + 12n
Решить уравнение 12x2 + 3x = 0.

Слайд 11

Рефлексия.
Мы ввели новое (для вас) понятие математического языка: разложение многочлена на множители. Вы познакомились с приемом разложения многочлена на множители:
вынесение общего множителя за скобки.

Слайд 12

Домашнее задание:
Правила выучить §3 (стр. 51-52), № 217 (4,5), № 218(1,2)