Презентация - Определение арифметической прогрессии - Формула n-го члена арифметической прогрессии

Слайд 1

Определение арифметической прогрессии.Формула n-го члена арифметической прогрессии
Козак Татьяна Ивановна, учитель математики МОБУ СОШ №20 пгт.Прогресс Амурской области
2014 г
Алгебра, 9 класс

Слайд 2

Повторение изученного
№1. Решите систему способом подстановки: х2 + у = 14 у – х = 8
№2. Найдите первые шесть членов последовательности, заданной формулой n-го члена: хn = 2n – 1

Слайд 3

Проверь себя
у = 8 + х х2 +8 + х – 14 = 0 х2 + х – 6 = 0 D = 1 + 4  1  6 = 25 х1 = 2; х2 = –3; у1 = 10; у2 = 5. Ответ: (2;10); (–3;5)
х1 = 2  1 – 1 = 1; х2 = 2  2 – 1 = 3; х3 = 2  3 – 1 = 5; х4 = 2  4 – 1 = 7; х5 = 2  5 – 1 = 9; х6 = 2  6 – 1 = 11.

Слайд 4

Последовательность чисел: 1; 5; 9; 13; 17; 21; … Каждый её член, начиная со второго, получается прибавлением к предыдущему члену числа 4. Такая последовательность является примером арифметической прогрессии. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

Слайд 5

Любой член арифметической прогрессии аn; Следующий член прогрессии аn+1; при любом n верно: аn+1 – аn= d Число d называют разностью арифметической прогрессии.

Слайд 6

Пример:
1) а1 = 5; d = 3. Найдите а2 и а3. а2 = а1 + d = 5 + 3 = 8; а3 = а2 + d = 8 + 3 = 11. 2) Назовите следующие три члена арифметической прогрессии. 14; 17; 20.
№575
№576

Слайд 7

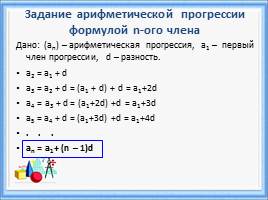
Задание арифметической прогрессии формулой n-ого члена
Дано: (аn) – арифметическая прогрессия, a1 – первый член прогрессии, d – разность. a2 = a1 + d a3 = a2 + d = (a1 + d) + d = a1+2d a4 = a3 + d = (a1+2d) +d = a1+3d a5 = a4 + d = (a1+3d) +d = a1+4d . . . an = a1+ (n – 1)d

Слайд 8

Формула n-го члена арифметической прогрессии
аn = а1 + d(n – 1)

Слайд 9

Пример №1
Последовательность (сn): с 1= 0,6; d = 0,4 Найдите 11-й член этой прогрессии. аn = а1 + d(n – 1) с11 = с1 + d(11 – 1) = с1 + 10d; с11 = 0,6 + 0,4  10 = 0,6 + 4 = 4,6.
№577
№579

Слайд 10

Д/з:
п.25; №578; №580; №601

Слайд 11

Определение арифметической прогрессии.Формула n-го члена арифметической прогрессии
Урок №2

Слайд 12

Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией
1; 2; 4; 9; 16; … 2; 4; 8; 16; … 1; 11; 21; 31; … 7; 7; 7; 7; …
Почему остальные не могут являться арифметической прогрессией?

Слайд 13

Определение
Разность
Формула n-го члена
Формулы арифметической прогрессии

Слайд 14

В какой фигуре записана арифметическая прогрессия?
Верно
Верно
Верно
Не верно
Не верно

Слайд 15

Определение
Разность
Формула n-го члена
Формулы арифметической прогрессии
№579(б)
№581
№584
№587

Слайд 16

Д/з:
п.25; №582; №585; №586

Слайд 17

Определение арифметической прогрессии.Формула n-го члена арифметической прогрессии
Урок №3

Слайд 18

Найдите первые четыре члена арифметической прогрессии, заданной формулой:
1) аn = 2n + 3 2) аn = 1 + 3n 3) аn = 5 – 2n
5; 7; 9; 11;…
4; 7; 10; 13;…
3; 1; -1; -3;…

Слайд 19

В арифметической прогрессии ( bп ) известны b1 = –12 и d = 3. Под каким номером находится член прогрессии, равный 0 ?

Слайд 20

Арифметическая прогрессия
an = kn + b, k и b – некоторые числа d = k
№597

Слайд 21

характеристическое свойство

Слайд 22

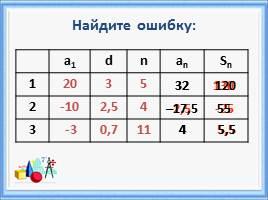
  а1 d n an Sn
1 20 3 5
2 -10 2,5 4
3  -3 0,7 11
Найдите ошибку:
130
-2,5
-25
32
4
5,5
32
120
–17,5
55
4
5,5

Слайд 23

Д/з:
п.25; №594; №588; №590; №592