Презентация - Разбор и решение задания №9 ОГЭ по математике

Слайд 1

Разбор и решение задания №9 ОГЭ по математике
Выполнила: ученица 9 класса Ж Новикова Анастасия

Слайд 2

Цель работы: Научиться решать задание №9 из ОГЭ модуля «Геометрия» Подкорректировать усвоенные знания, умения и навыки.

Слайд 3

Так как задания №9 основаны на теории по теме "треугольники", рассмотрим базовые понятия, определения и формулы. Вначале предлагаю рассмотреть углы на плоскости:
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Внутренние односторонние углы - это углы, которые лежат внутри между прямыми по одну сторону от секущей.

Слайд 4

Многие задачи построены на нахождении медиан и биссектрис треугольника: Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам. Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам. Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

Слайд 5

Медиана:

Слайд 6

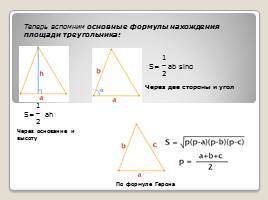
Теперь вспомним основные формулы нахождения площади треугольника:
1  2
ah
S=
S=
1  2
ab sinα
Через основание и высоту
Через две стороны и угол
По формуле Герона

Слайд 7

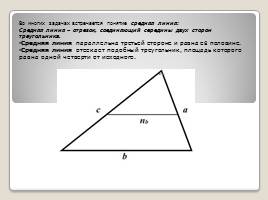
Во многих задачах встречается понятие средняя линия: Средняя линия – отрезок, соединяющий середины двух сторон треугольника. Средняя линия параллельна третьей стороне и равна её половине. Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

Слайд 8

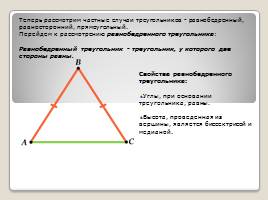
Теперь рассмотрим частные случаи треугольников - равнобедренный, равносторонний, прямоугольный. Перейдем к рассмотрению равнобедренного треугольника: Равнобедренный треугольник - треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника: Углы, при основании треугольника, равны. Высота, проведенная из вершины, является биссектрисой и медианой.

Слайд 9

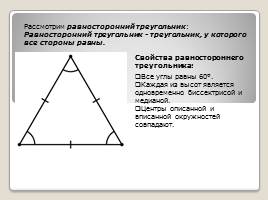
Рассмотрим равносторонний треугольник: Равносторонний треугольник - треугольник, у которого все стороны равны.
Все углы равны 60°. Каждая из высот является одновременно биссектрисой и медианой. Центры описанной и вписанной окружностей совпадают.
Свойства равностороннего треугольника:

Слайд 10

Прямоугольный треугольник
Треугольник называется прямоугольным, если один из его углов прямой.
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. Для прямоугольного треугольника справедливы следующие утверждения:
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Сумма острых углов треугольника равна 90:
Катет, лежащий против угла, равен половине гипотенузы. Две высоты прямоугольного треугольника совпадают с его катетами. Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Слайд 11

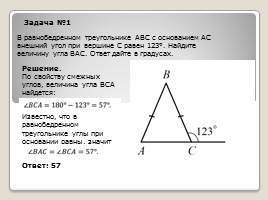
В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.
Задача №1
Решение. По свойству смежных углов, величина угла ВСА найдется: Известно, что в равнобедренном треугольнике углы при основании равны, значит Ответ: 57

Слайд 12

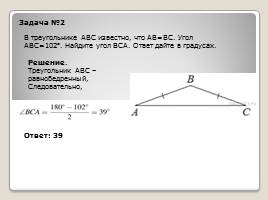
Задача №2
В треугольнике ABC известно, что АВ=ВС. Угол АВС=102. Найдите угол ВСА. Ответ дайте в градусах.
Решение. Треугольник АВС – равнобедренный, Следовательно,
Ответ: 39

Слайд 13

Задача №3
В треугольнике ABC АВ=ВС=15, АС=24. Найдите длину медианы ВМ.
Решение. Треугольник АВС – равнобедренный, поэтому медиана, проведенная к основанию, является биссектрисой и высотой. Из прямоугольного треугольника АВМ по теореме Пифагора найдем ВМ:
Ответ: 9

Слайд 14

Задача №4
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Решение
Формула площади для прямоугольного треугольника выглядит следующим образом: Площадь прямоугольного треугольника равна половине произведения его катетов. Это следует из того, что один из катетов является высотой к основанию, которым является второй катет. Следовательно, S = ½ • 15 • 4 = 30
Ответ:30

Слайд 15

Задача №5
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Решение
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой. Для медианы, а значит и для высоты, формулу я приводил чуть выше: m = ( a • √3 )/ 2 Подставим значение: m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18 Ответ: 18.