Презентация - Реализация компетентностного подхода на уроках математики

Слайд 1

реализация компетентностного подхода при обучении математике в средней школе

Слайд 2

Цель работы: анализ теоретических аспектов компетентностного подхода и разработка методических рекомендаций по составлению задач для формирования ключевых компетенций учащихся при обучении математике в средней школе.

Слайд 3

Задачи:
1. Провести анализ основных понятий компетентностного подхода в образовании; 2. Выявить и охарактеризовать ключевые компетенции при обучении математике; 3. Рассмотреть методические аспекты реализации компетентностного подхода в практике обучения математике; 4. Разработать методические рекомендации по составлению и использованию задач для формирования ряда ключевых компетенций школьников на уроках математики.

Слайд 4

Компетенция – это совокупность взаимосвязанных качеств личности (знаний, умений, навыков, способов деятельности), задаваемых по отношению к определенному кругу предметов и процессов и необходимых, чтобы качественно продуктивно действовать по отношению к ним. Компетентность – владение, обладание человеком соответствующей компетенцией, включающей его личностное отношение к ней и предмету деятельности.

Слайд 5

Ключевые компетенции: ценностно-смысловая, общекультурная, учебно-познавательная, информационная, коммуникативная, социально-трудовая, компетенция личностного самосовершенствования.

Слайд 6

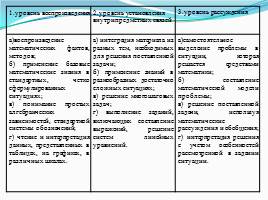
1.уровень воспроизведения 2.уровень установления внутрипредметных связей 3.уровень рассуждения
a)воспроизведение математических фактов, методов; б) применение базовые математические знания в стандартных, четко сформулированных ситуациях; в) понимание простых алгебраических зависимостей, стандартной системы обозначений; г) чтение и интерпретация данных, представленных в таблицах, на графиках, в различных шкалах. а) интеграция материала из разных тем, необходимых для решения поставленной задачи; б) применение знаний в разнообразных достаточно сложных ситуациях; в) решение многошаговых задач; г) выполнение заданий, включающих составление выражений, решение систем линейных уравнений. а)самостоятельное выделение проблемы в ситуации, которая решается средствами математики; б) составление математической модели проблемы; в) решение поставленной задачи, используя математические рассуждения и обобщения; г) интерпретация решения с учетом особенностей рассмотренной в задании ситуации.

Слайд 7

Ключевская Сопка – самый высокий вулкан Камчатки – на 4750 м. выше уровня моря. Гора Белуха на Алтае на 244 м. ниже Ключевской Сопки. Гора Народная на Урале на 2612 м. ниже Белухи, а гора Победа (хребет Черского) на 1253 м. выше Народной. Какова высота горы Победа? На сколько метров Ключевская Сопка выше горы Победа? Постройте столбчатую диаграмму, изображающую распределение высоты гор?

Слайд 8

Начертите таблицу, в первом столбце которой перечислите все месяцы года, а во втором – число детей, родившихся в течение каждого месяца
Используя диаграмму, ответьте на вопросы: а) в каком месяце в селе родилось больше всего детей; б) в каком месяце в селе родилось столько же детей, сколько в апреле; в) в какие месяцы родилось по два ребенка; г) сколько детей родилось в марте; д) сколько детей родилось за первую половину года; е) сколько детей родилось за весь год.

Слайд 9

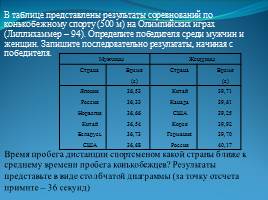
Время пробега дистанции спортсменом какой страны ближе к среднему времени пробега конькобежцев? Результаты представьте в виде столбчатой диаграммы (за точку отсчета примите – 36 секунд)
В таблице представлены результаты соревнований по конькобежному спорту (500 м) на Олимпийских играх (Лиллихаммер – 94). Определите победителя среди мужчин и женщин. Запишите последовательно результаты, начиная с победителя.
Мужчины Мужчины Женщины Женщины
Страна Время (с) Страна Время (с)
Япония Россия Норвегия Китай Беларусь США 36,53 36,33 36,66 36,54 36,73 36,68 Китай Канада США Корея Германия Россия 39,71 39,61 39,25 39,92 39,70 40,17